C++ OpenGL Physics Simulation

Kate LaHorgue and I teamed up for our final project for CS 175 (Computer Graphics). We were interested in taking our sandbox further and implementing a physics simulation, specifically addressing collision detection and conservation of momentum with planes and spheres. Read the republished writeup below, then hop over to Bitbucket to see the C++/OpenGL source code.

Authors: Nicolas Chavez, Kate LaHorgue

Course: Harvard CS 175

Instructor: Professor Steven Gortler

TF: Yuanchen Zhu

Instructions

To run our project, compile using make and then run ./asst10. At startup, there is no gravity or damping factor, so the simulation represents perfectly elastic collisions in a vacuum. Use the ‘g’ key to toggle gravity and inelastic collisions for a more physically realistic simulation.

Use the ‘k’ key to pause and play the simulation. Pressing ‘p’ and then clicking on one of the planes or spheres makes that geometry active, so you can reposition it. Pressing ‘v’ makes the camera the active object again.

Basic Process

Each time it’s run, our program generates 10 spheres of random color, radius, and velocity (you can change the variable g_numSpheres at the top of asst10.cpp to simulate more or fewer spheres — we’ve found that the simulation starts to slow down after about 60 spheres). We calculate each sphere’s mass as 4 ⁄3 π r³ · g_density and set its acceleration to (0, 0, 0). When gravity is activated, it changes each sphere’s acceleration to (0,-g,0).

In each iteration of the timed callback function updateSimulation, we update each sphere’s velocity due to its acceleration, and update its position due to its velocity. We then check every sphere against every plane and every other sphere to see if there have been any collisions. If two geometries have collided, we update their velocities using either updateSphereSphereVelocities or updateSpherePlaneVelocities.

Physics Concepts

Sphere-Sphere Collisions

Spheres are defined as a position, representing the center of the sphere, and a radius. If two spheres with radii r₁ and r₂ are intersecting, it means that the distance between their centers is less than r₁ + r₂ . So to check for collisions between spheres, we just find the world positions of the center of each sphere using getPathAccumRbt and then calculate the distance between them.

After a collision, each sphere’s new velocity can be found by accounting for conservation of momentum and kinetic energy; that is, if we have spheres of masses m₁ and m₂, with original velocities u₁ and u₂, then their new velocities v₁ and v₂ must satisfy

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

and

½ m₁(u₁ · u₁) + ½ m₂(u₂ · u₂) = ½ m₁(v₁ · v₁) + ½ m₂(v₂ · v₂)

Since the change in momentum is in the direction of the normalized vector k connecting the spheres’ centers, we can simplify these equations to get the new velocities

v_1 = u_1 - \left(\frac{2k \cdot(u_1 - u_2)m_2}{m_1 + m_2}\right)k

v_2 = u_2 + \left(\frac{2k \cdot(u_1 - u_2)m_1}{m_1 + m_2}\right)k

Sphere-Plane Collisions

Planes are defined in term of their normal, a position for their center, and how wide and long they are. Therefore, to calculate the intersection, the world position of the center of the plane is calculated using getPathAccumRbt and then the sphere center is calculated the same way. Then, the line parallel to the plane’s normal that passes through the sphere’s center is checked to see where it intersects with the plane. By getting the distance from the point of this line’s intersection to the center of the sphere, we are getting the closest distance the sphere is to the plane. If this distance exceeds the radius of the sphere, it is intersecting. Then, we need to check that this is happening within the plane’s bounds – we simply do a change of basis to check that the intersection point is within the bounds.

The planes in our simulation are stationary, so to calculate the new velocity of a sphere after colliding with a plane we just reflect the velocity vector of the sphere around the plane’s normal vector. The reflection calculation is represented in the following diagram:

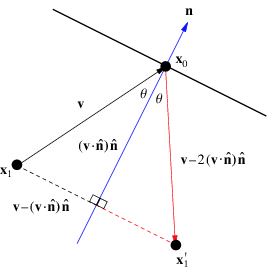
So for a sphere with velocity v and a plane with (unit-length) normal vector n, the new velocity is v - 2(v · n) n.

Damping

Collisions aren’t always perfectly elastic — there’s usually some loss of kinetic energy during the collision. When damping is activated, we keep a damping constant and multiply each new velocity v by (1 - damping) after a collision so the spheres eventually slow to a stop.

Data Structures

PhysicsBody

The PhysicsBody class encapsulates the acceleration, velocity, mass, and shape of an object. It exists to separate the graphics logic from the simulation logic. This is an abstract class, however; the concrete subclasses follow.

SphericalPhysicsBody

Defined only by a radius.

PlanarPhysicsBody

Defined by a length, a width, and a unit normal to determine the orientation of the plane.

HasPhysicsBody

An interface that can return a PhysicsBody and can have its RigTForm updated. This is used by the PhysicsSim class in order to only deal with position and physics updates.

PhysicsSim

Is called regularly to update the state of the HasPhysicsBody objects it accumulates via the ‘add’ function. It checks sphere-sphere collisions and sphere-plane collsions, updating the objects as a result of this. The setDamping method changes the proportion of velocity retained at every collision, simulating inelastic collision.

Issues + Solutions

One issue we discovered when running our simulation was that in certain cases, spheres would stick together rather than rebounding after a collision. The video below shows this phenomenon, where the intersecting spheres rotate around each other instead of separating:

We fixed this issue by including a position correction when checking for collisions between spheres. If we find that two spheres have intersected, we take the vector between their centers and back one of the spheres up along that vector until the two shapes no longer intersect. This way, the spheres never truly intersect, so we don’t have to worry about them sticking together. In fact, if we intentionally make two spheres occupy the same space, this fix automatically separates them:

We encountered a similar problem with spheres becoming embedded in planes, especially when gravity and damping were activated:

We used a similar strategy to fix this issue, backing the sphere up along the vector normal to the plane at the intersection point until it no longer intersects the plane. Again, if we intentionally embed a sphere into a plane, the simulation will automatically correct its position:

More Videos

Simulation at startup — elastic collisions in a vacuum (Note: the fourth wall of the box is situated right in front of the camera, so the spheres bounce off of it, but it’s not shown since it’s facing away from the camera):

With walls at different angles:

With gravity and damping added:

With gravity and sloped ground:

Cool flat shading makes it look like a screensaver!

Resources

Vector reflection: Wolfram Alpha

Elastic collision velocity derivation: SJSU

Appendix

Source Code on BitBucket